
In diesem Ratgeber erklären wir die Prozentrechnung. Außerdem findest Du eine Eselsbrücke, damit Du Dir die Prozentformel leichter merken kannst. Und wir haben einen Spickzettel, der Dir das Leben noch ein bisschen einfacher macht.
- Prozentrechnung einfach erklärt
- Zum Online-Prozentrechner
- Direkt zum Spickzettel
- Zur Eselsbrücke für die Grundformel
Was bedeutet eigentlich 100 Prozent?
Du kennst bestimmt den Satz: „Streng Dich mal an, gib 100 Prozent!“ Aber was genau heißt „100 Prozent“? Was sind denn überhaupt Prozentzahlen?
Hundert Prozent sind „ein Ganzes“. 100 Prozent einer Tafel Schokolade sind also die ganze Tafel. Mit „100 Prozent geben“ meint man deshalb: „Gib alles!“ (Dein Ganzes).
Das mathematische Symbol für Prozent ist %.

Woher kommt das Wort – „Prozent“?
Prozent kommt aus dem lateinischen („pro centum“). Es bedeutet: „von Hundert“ oder „Hundertstel“. Im Matheunterricht muss man in Sachaufgaben oft die Prozentzahlen der verrücktesten Sachen berechnen. Im echten Leben werden Prozente meist bei Rabatt, Statistiken oder Zinsen verwendet.
Mathematisch legen wir bei jeder Aufgabe fest, was das Ganze (=100 %) sein soll. Das können Zahlen, Schokoladentafeln, Geldbeträge usw. sein, die also Hundert von Hundert sind:
\text{ 100\,\% }=\frac{ 100 }{ 100 }=\text{ Hundert von Hundert }=\text{ 1 }Ein Prozent vom Ganzen ist also genau ein Hundertstel:
\text{ 1\,\% }=\frac{ 1 }{ 100 }=\text{ 1 Teil von Hundert }=\text{ 0,01 }3 % sind 3 Teile von Hundert oder auch 3 Hundertstel. Beispiel: Dass 3 % nicht viel sind, weiß jeder, der nur noch 3 % Akku übrig hat.
\text{ 3\,\% }=\frac{ 3 }{ 100 }=\text{ 3 Teile von Hundert }=\text{ 0,03 }Ein Viertel, drei Viertel, die Hälfte
Ein Viertel ist 25 % des Ganzen, die Hälfte ist 50 % und 75 % sind drei Viertel. Weshalb das so ist, zeigen wir hier:
\text{ 75\,\% }=\text{ 75 Teile von 100 }= \frac{ 75 }{ 100 }=\frac{ 75:25 }{ 100:25 }=\frac{ 3 }{ 4 }=\text{ 0,75 }Das Kürzen eines Bruchs (hier : 25) erklären wir Dir weiter unten noch genauer.
Genauso funktioniert das bei 25 %:
\text{ 25\,\% }=\text{ 25 Teile von 100 }= \frac{ 25 }{ 100 }=\frac{ 25:25 }{ 100:25 }=\frac{ 1 }{ 4 }=\text{ 0,25 }Und bei 50 % erhalten wir „ein Halbes“, also die Hälfte des Ganzen:
\text{ 50\,\% }=\text{ 50 Teile von 100 }= \frac{ 50 }{ 100 }=\frac{ 50:50 }{ 100:50 }=\frac{ 1 }{ 2 }=\text{ 0,5 }Hier erklären wir genau, wie Du einen Bruch kürzen kannst:
Die Zahl über dem Bruchstrich ist der Zähler, die Zahl unter dem Bruchstrich nennt man Nenner. Beim Kürzen suchen wir eine Zahl, durch die Du sowohl den Zähler als auch den Nenner teilen kannst. Dadurch wollen wir den Bruch einfacher machen (Bruchrechner hier).
Beispiel von oben:
75 %: 75 Prozent sind 75 von 100. Diesen Bruch kann man vereinfachen (kürzen): Man teilt den Zähler über dem Bruchstrich, die 75, und den Nenner unter dem Bruchstrich, die 100, durch 25. Dann bleibt oben die 3 und unten die 4 stehen. Deshalb sind 75 % auch drei Viertel:
Etwas schwierigeres Beispiel:
45 %: 45 Prozent sind 45 von 100. Diesen Bruch kannst Du so kürzen: Du teilst den Zähler über dem Bruchstrich, die 45, und den Nenner unter dem Bruchstrich, die 100, jeweils durch 5. Dann bleibt oben die 9 und unten die 20 übrig:
Hier kannst Du nicht weiter kürzen. Als Ergebnis bleiben 9 Teile von 20 stehen. Manchmal musst Du etwas herumprobieren, bis Du den kleinstmöglichen Zähler und Nenner erhältst. Du kannst auch in mehreren Schritten kürzen:
Beispiel 60 %:
\text{ 60\,\% }=\frac{ 60 }{ 100 }Schritt 1:
\frac{ 60:10 }{ 100:10 }=\frac{ 6 }{ 10 }Schritt 2:
\frac{ 6:2 }{ 10:2 }=\frac{ 3 }{ 5 }Begriffe in der Prozentrechnung: Was bedeutet was?
Wenn manchmal Deine Eltern bei den Hausaufgaben helfen oder Du Dir ab und zu ein Mathe-Tutorial auf YouTube anschaust, hast Du hundertprozentig schon mal gesagt oder gedacht: „Häh? Dieses Wort hat mein Lehrer noch nie benutzt, der nennt das alles ganz anders!“
Tatsächlich werden oft unterschiedliche Ausdrücke für dieselbe Sache verwendet. Der Mathe-Lehrer einer Klasse benutzt vielleicht dieses Wort, der Lehrer einer anderen Klasse meint dasselbe, benutzt aber ein anderes Wort. Die Eltern wiederum haben etwas ganz anderes gelernt. Das kann sehr verwirrend sein.
Deshalb haben wir hier die drei Hauptbegriffe der Prozentrechnung und deren Synonyme aufgeführt. Synonyme heißen die Wörter, die manchmal stattdessen benutzt werden, aber dasselbe meinen.
| Hauptbegriff | Manche sagen auch | Abkürzung |
|---|---|---|
| Grundwert | Basis, Ausgangswert | G |
| Prozensatz | Prozent, prozentualer Anstieg oder Reduktion | P, p oder p% |
| Prozentwert | absoluter Anstieg oder Reduktion | W |
Prozentsatz, Prozentwert und Grundwert
- Prozentsatz (P): Der Prozentsatz sagt aus, wie viele Teile von Hundert gemeint sind. Er legt also den Anteil fest. Du erkennst den Prozentsatz in Matheaufgaben meistens am Prozentsymbol %. In einer Rechenformel schreiben einige für den Prozentsatz nur ein P, manche aber auch P %.
Beispiel: 5 % von 100 = 5. - Prozentwert (W): Der Prozentwert ist das „Ergebnis“. Wenn Du den Anteil (p) vom Grundwert berechnet, dann erhältst Du den Prozentwert.
Beispiel: 5 % von 100 = 5. - Grundwert (G): Der Grundwert ist der Wert, von dem genau der Anteil (p) genommen wird. Du erkennst den Grundwert in Matheaufgaben häufig am Wort „von“.
Beispiel: 5 % von 100 = 5.
Eselsbrücke für Prozentrechnung: Die Grundformel
Jetzt wissen wir also, was Prozent bedeutet – aber wie rechnen wir damit? Das Gute ist: Alle Prozentrechnungen lassen sich von einer einzigen Formel ableiten. Egal, ob Du den Prozentsatz (P), den Prozentwert (W) oder den Grundwert (G) suchst. Diese Formel kannst Du immer benutzen, wenn Du sie entsprechend umstellst. Eigentlich brauchst Du nur diese Grundformel kennen:
Wie Du die Formel umstellen musst, erklären wir im nächsten Kapitel. Jetzt verraten wir Dir erst einmal einen super Trick, um Dir die Grundformel zu merken. Mit dieser Eselsbrücke kannst Du Dich bestimmt immer daran erinnern:

Als druckbare PDF-Datei downloaden
Lies Dir diese Eselsbrücke ruhig ein paar Mal durch. Versuche sie Dir zu merken. Und dann lies sie Dir noch ein paar Mal durch. Unser Gehirn lernt durch Wiederholung.
Nach 100 mal (W)orkout macht (G)roßmutter mal (P)ause
Nachdem wir uns die Grundformel gemerkt haben, schauen wir uns an, was sie eigentlich bedeutet. Dabei nehmen wir die Formel einmal komplett auseinander:
100 = 100 Prozent
mal = das Mal-Zeichen, also der Multiplikator in der Formel (x)
(W)orkout = W – der Prozentwert
macht = das Gleichheitszeichen („ist gleich“, =)
(G)roßmutter = G – Grundwert
mal = wieder das Mal-Zeichen
(P)ause = P – Prozentsatz
Je nachdem, was Du ausrechnen willst, muss die Formel jetzt umgestellt werden. Lies weiter, dann erfährst Du mehr.
Prozentsatz-Formel erklärt: Wie viel % sind 50 von 200 ?
Der Prozentsatz (P) verrät, wie viel Prozent zum Beispiel 50 von 200 sind. 50 ist der Prozentwert (W) und 200 ist der Grundwert (G).
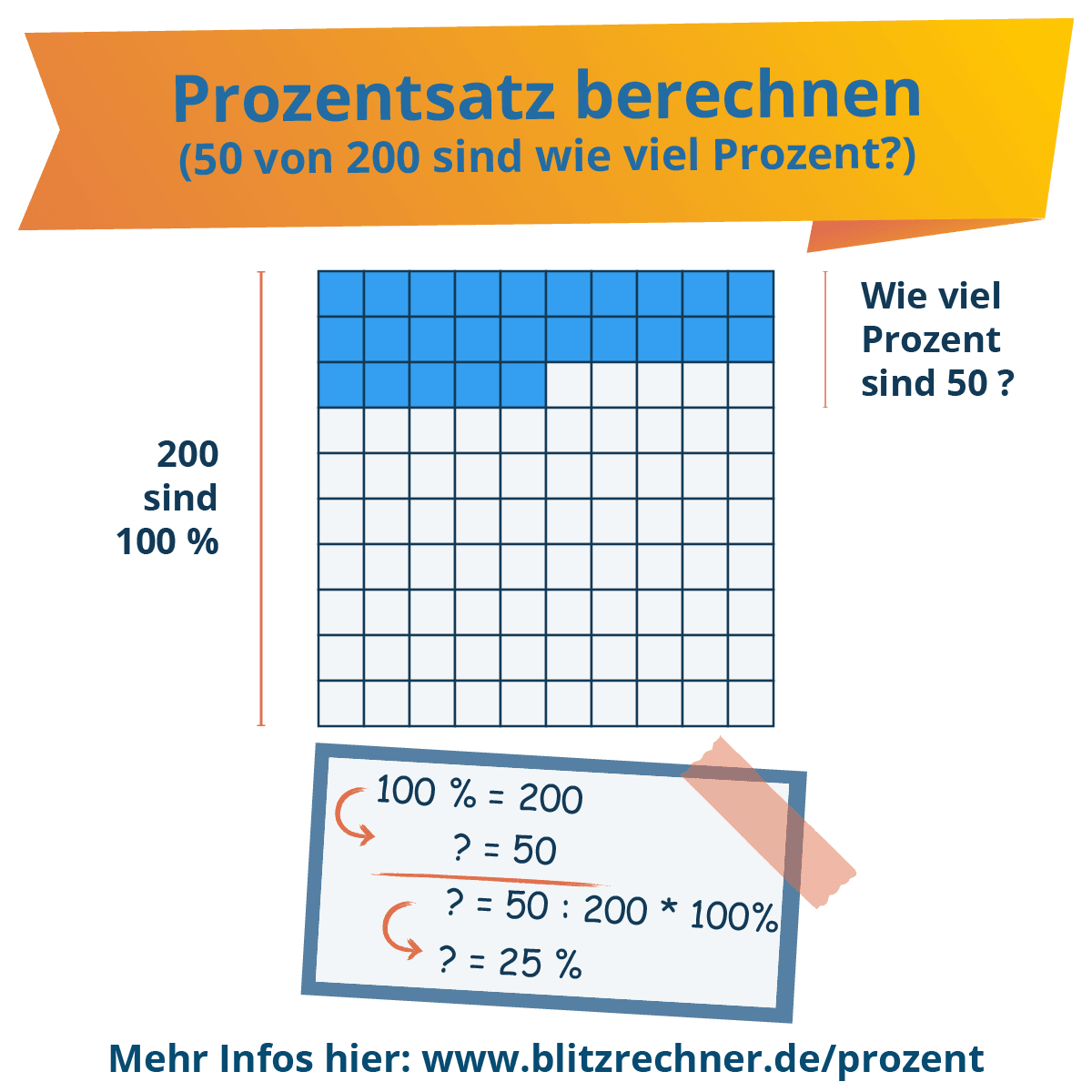
Die Prozentsatz-Formel
Dein Mathelehrer formuliert es wahrscheinlich so: Der Prozentsatz ergibt sich aus der Division des Prozentwerts (Dividend) durch den Grundwert (Divisor) und der anschließenden Multiplikation mit 100 %.
Häh? Genau deshalb erklären wir Dir die Prozentsatz-Formel jetzt Schritt für Schritt:
- Bei der Frage „Wie viel % sind 50 von 200?“ wird der Prozentsatz (P) gesucht
- Wir kennen den Prozentwert (W) = 50
- Und den Grundwert (G) = 200
Jetzt müssen wir die Grundformel umstellen. Falls Du nicht mehr weißt, wie das geht, schaue Dir das Video hier an.
Dafür teilen wir durch G, damit P allein stehen bleibt – denn das wollen wir ja ausrechnen. Somit erhalten wir:
Das ist die Prozentsatz-Formel. In diese setzen wir jetzt einfach die Werte ein:
Zuerst rechnen wir 50 geteilt durch 200, das Ergebnis ist 0,25. Das setzen wir statt des Bruchs (50/200) in die Formel ein:
Dann multiplizieren wir mit 100 %, um den Prozentsatz zu erhalten.
Fertig:
So einfach geht’s: 50 (Prozentwert) von 200 (Grundwert) sind also 25 % (Prozentsatz) .
Prozentwert-Formel erklärt: Wie viel sind 25 % von 200 ?
Es gibt ein paar Ergebnisse, die kann man noch leicht im Kopf ausrechnen. Zum Beispiel 50 % von 100: 50 % ist die Hälfte. Die Hälfte von 100 ist 50. 50 ist hier der Prozentwert (W).
Auch dieses Beispiel ist recht einfach: Wenn man 10 % von 100 haben will, dann sind das 10.
Setzen wir jetzt die mathematischen Begriffe ein, lautet der Satz:
Wenn man 10% (Prozentsatz) von 100 (Grundwert) haben will, dann sind das 10 (Prozentwert). Damit sind wir der Prozentwert-Formel schon auf der Spur.

Die Prozentwert-Formel
Dein Mathelehrer verwirrt Dich vielleicht mit einem Satz wie: „Das Ergebnis der Multiplikation von Prozentsatz und Grundwert geteilt durch 100 ergibt den Prozentwert.“
Keine Panik, das geht auch einfacher. Nämlich so:
- Wir wollen wissen, wie viel 25 % von 200 sind. Wir suchen also den Prozentwert (W)
- Der Prozentsatz ist 25 % (P)
- Der Grundwert ist 200 (G)
Wir haben uns ja die Grundformel
gemerkt und stellen diese wieder um. Dafür teilen wir durch 100 %, damit W allein stehen bleibt – denn W möchten wir am Ende ausrechnen. Die Prozentwert-Formel lautet also:
Nun setzen wir einfach die Werte ein:
Das Ergebnis lautet:
25 % (Prozentsatz) von 200 (Grundwert) sind also 50 (Prozentwert).
Grundwert-Formel erklärt: 50 sind 25 % von wie viel?
Wenn wir wissen, dass 50 genau 25 % von einem Wert sind, dann bezeichnet man diesen als Grundwert (oder auch Ausgangswert). Unter dem Grundwert (G) versteht man also das Ganze, auf das sich die Prozentangaben beziehen. Und diesen Grundwert kann man ausrechnen. Wir verraten Dir, wie.

Die Grundwert-Formel
Kompliziert wird es in Schulbüchern oder im Matheunterricht manchmal so ausgedrückt: Den Grundwert (G) erhält man, indem man den Prozentwert (W) durch den Prozentsatz (P) dividiert und anschließend mit 100 % multipliziert.
Geht das auch einfach? Aber klar, wir erklären es Dir Schritt für Schritt:
- Bei der Frage „50 sind 25 % von wie viel“ ist der Grundwert (G) der gesuchte Wert.
- Der Prozentwert (W) ist 50.
- Der Prozentsatz ist 25 %.
Weil wir uns nur die Grundformel
gemerkt haben, stellen wir diese zuerst um. Wir teilen durch P, damit G allein stehen bleibt, denn G wollen wir ja ausrechnen. Dadurch erhalten wir die Grundwert-Formel:
Dann setzen wir die obigen Werte ein:
Und erhalten das folgende Ergebnis:
50 (Prozentwert) ist also 25 % (Prozentsatz) von 200 (Grundwert).
Pst! Spickzettel zur Prozentrechnung
Mit der Eselsbrücke oben kann man sich die Grundformel der Prozentrechnung gut merken, da braucht man gar keinen Spickzettel. Und von der Grundformel lassen sich alle anderen Formeln einfach ableiten. Wenn Du allerdings nicht sicher bist, ob Dein Gehirn unter Prüfungsstress noch genauso gut funktioniert wie jetzt gerade: Wir haben Dir die drei Formeln noch mal als Spickzettel zusammengestellt.
Natürlich weißt Du, dass spicken verboten ist. Trotzdem haben wir die Formeln mal so kleingeschrieben, dass sie theoretisch prima in eine Hosentasche oder ein Mäppchen passen. Meistens reicht es schon, kurz vor der Mathearbeit einfach nochmal draufzuschauen. Viel Glück, Du packst das!
Hier kannst Du den Spicker zur Prozentrechnung herunterladen (PDF)
- Dreisatz: Der Rechner plus allen Formeln und Erklärungen
- Bruchrechnen: Schnell ausrechnen oder richtig lernen – hier geht beides
FAQ
Welche sind die drei Formeln der Prozentrechnung?
Prozentsatz-Formel:
Prozentsatz (P)=Prozentwert (W)/Grundwert (G)×100 %
Prozentwert-Formel
Prozentwert (W)=Grundwert(G)×Prozentsatz(P)/100 %
Grundwert-Formel
Grundwert (G)= Prozentwert (W)/Prozentsatz (P)×100 %
Hier geht es zu den Prozent-Rechnern.
Wie rechnet man die Prozentrechnung?
Du möchtest etwas kaufen und bekommst es zum Beispiel 20 % günstiger? Dann nimmst Du den Kaufpreis (Grundwert), teilst ihn durch 20 (Prozentsatz) und multiplizierst mit 100 %. Mehr Infos zum ermittelten Prozentwert.
Wie rechnet man etwas in Prozent aus?
Du willst wissen, wie viel % ein bestimmter Anteil von einem Wert genau sind? Dann nimmst Du den Wert, teilst ihn durch den Anteil und multiplizierst mit 100 %. Hier die Formeln der Prozentrechnung.
Wie rechnet man aus, wie viel der ursprüngliche Wert war?
Du kennst den Prozentsatz und den entsprechenden Betrag? Prima, Du nimmst einfach den Betrag (Prozentwert), teilst durch den Prozentsatz und multiplizierst mit 100 %. Mehr zur Grundwert-Formel
Wie geht die Formel für Prozentrechnung?
So lautet die Grundformel: 100 % × W (Prozentwert) = G (Grundwert) × P (Prozentsatz).
Diese Formel kannst Du mit unseren Hinweisen einfach umstellen. Hier geht es zur „Eselsbrücke“ und den drei Formeln der Prozentrechnung.

