 Hallo! Schön, dass du da bist! In den nächsten 12 Sekunden lösen wir deine Prozentfrage. Nutze den super-einfachen Online-Prozentrechner. Oder schau dir unsere Prozentformeln, Rechenwege und Beispiele an.
Hallo! Schön, dass du da bist! In den nächsten 12 Sekunden lösen wir deine Prozentfrage. Nutze den super-einfachen Online-Prozentrechner. Oder schau dir unsere Prozentformeln, Rechenwege und Beispiele an.
Prozentrechner
Prozentwert, Prozentsatz, Grundwert
Prozent-Rechner für Dummies
Du willst mit dem ganzen Mathe-Zeug nichts zu tun haben, sondern einfach nur ein Ergebnis wissen ohne selbst Prozentrechnen zu müssen? Dann gib einfach die Zahlen in unseren Online-Prozentrechner ein, wir finden alle richtigen Ergebnisse für Dich heraus!
Prozent selbst ausrechnen: Was möchtest du wissen?
- Achtung: Mehrwertsteuer abziehen oder draufschlagen »
- Rabatt-Rechner: Rabatte einfach berechnen
Teile vom Ganzen berechnen:
- Wie viel sind 25 % von 200? Prozentwert ermitteln »
- Wie viel % sind 50 von 200? Prozentsatz finden »
- 50 sind 25 % von wie viel? Grundwert berechnen »
Prozentuale Veränderungen berechnen:
- Wie viel % mehr/weniger sind 200 als 50? Von Wert zu Wert »
- Wie viel sind 50 zuzüglich/abzüglich 25 %? Prozent abziehen/aufschlagen »
- 200 sind 25 % mehr/weniger als wie viel? Ausgangswert finden »
Weiterführendes:
- Prozentrechnung einfach erklärt
- Dreisatz-Rechner: Mit dem Dreisatz kann man Prozent auch ausrechnen
- Brüche in Prozent oder Dezimalzahlen umrechnen
- Bruch-Rechner
Prozent-Formel
W = Prozentwert, G = Grundwert und P = Prozentsatz
Ausführliche Erklärungen zur Formel hier.
Warum braucht man überhaupt Prozent?
Prozentrechnung ist die Königsdisziplin der Alltagsmathematik: Prozente treten im täglichen Leben zwar an allen Ecken und Enden auf, dennoch ist die Mehrheit der Bevölkerung mit ihnen überfordert.
Prof. Dr. Christian Hesse, Autor und Professor im Fachbereich Mathematik, Universität Stuttgart
Teile vom Ganzen berechnen
Bei den folgenden Prozentrechnungen möchten wir wissen, wie viel ein Teil vom Ganzen ist. Prozentuale Veränderungen werden weiter unten erklärt.
Prozentwert berechnen: Wie viel sind 25 % von 200 ?
Okay, 50 % von 100 sind die Hälfte von 100, also 50. Doch wie berechnet man 25 % von 200? Um das auszurechnen, kannst du unseren Prozentwert-ermitteln-Rechner nutzen. Oder du liest dir den unteren Abschnitt mit den Formeln und Erklärungen durch und kommst zukünftig ohne technische Hilfe aus.

Öffnen, um die Formel zu verstehen
Okay. Und jetzt noch mal ganz einfach, Schritt für Schritt:
Der Prozentwert (W) ist der gesuchte Wert: Wir wollen wissen, wie viel 25 % von 200 sind.
Der Grundwert ist 200 (G). Der Prozentsatz ist 25 % (P).
Damit man sich nur eine Formel merken muss, stellen wir die Ausgangsformel
\text{100 \%}\times\text{W}=\text{G}\times\text{P}
erst einmal um. Wir teilen durch 100 %, damit W alleine stehen bleibt. Somit erhalten wir:
\text{Prozentwert (W)}=\text{Grundwert (G)}\times\frac{\text{Prozentsatz (P)}}{\text{100} \%}
Nun setzen wir einfach die Werte ein:
\text{Prozentwert (W)}=\text{200}\times\frac{\text{25} \%}{\text{100} \%}
Und wandeln den Bruch in eine Dezimalzahl um, indem wir einfach die 25 % durch die 100 % teilen:
\text{Prozentwert (W)}=\text{200}\times\text{0,25}
Schließlich rechnen wir 200 mal 0,25 und das Ergebnis lautet:
\text{Prozentwert (W)}=\text{50}
Antwort: 25 % (Prozentsatz) von 200 (Grundwert) sind also 50 (Prozentwert)!
Noch nicht verstanden? Hier eine noch einfachere Erklärung.
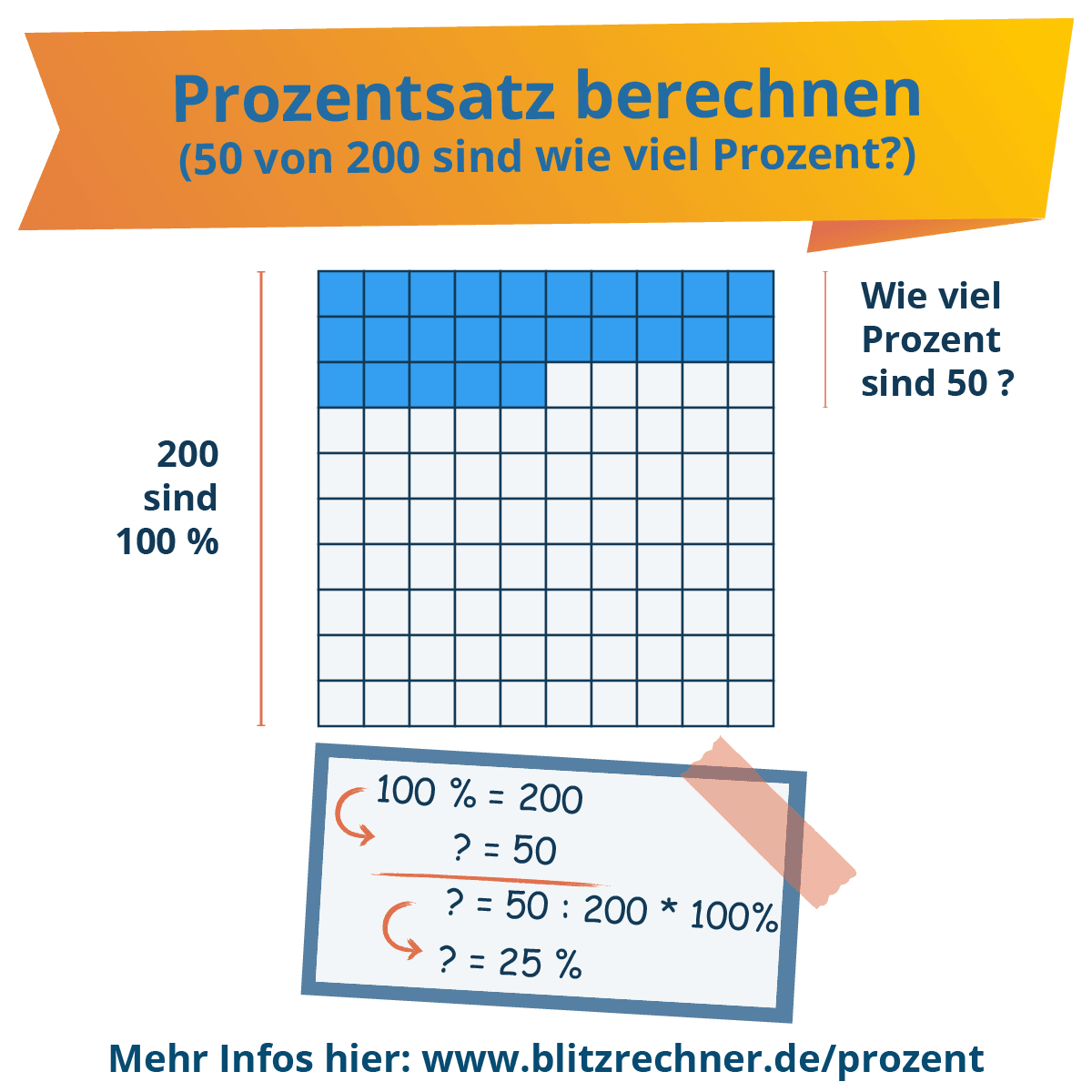
Prozentsatz berechnen: Wie viel % sind 50 von 200 ?
Klar, 50 von 100 sind die Hälfte, also 50 %. Doch wie berechnet man, wie viel Prozent 50 von 200 sind? Das kannst du ganz einfach mit dem Prozentsatz-finden-Rechner ausrechnen – oder du schaust dir die Formeln und Erklärungen unter dem Rechner an.
Öffnen, um die Formel zu verstehen
Und jetzt noch mal ganz einfach, Schritt für Schritt:
Der Prozentsatz (P) ist in diesem Fall der gesuchte Wert: Die Frage ist, wie viel Prozent 50 von 200 sind.
Der Prozentwert (W) ist 50. Der Grundwert (G) ist 200.
Damit man sich nur eine Formel merken muss, stellen wir die Ausgangsformel um:
\text{100 \%}\times\text{W}=\text{G}\times\text{P}
Wir teilen durch G, damit P alleine stehen bleibt – denn das ist ja der Wert, den wir hier suchen. Somit erhalten wir:
\text{Prozentsatz (P)}=\frac{\text{Prozentwert (W)}}{\text{Grundwert (G)}}\times\text{100 \%}
Jetzt setzen wir einfach die Werte ein:
\text{Prozentsatz}=\frac{\text{50}}{\text{200}}\times\text{100 } \%
Und rechnen die 50 geteilt durch 200 und setzen das Ergebnis (0,25) statt dem Bruch (50/200) in die Formel ein.
\text{Prozentsatz}=\text{0,25}\times\text{100} \%
Dann nur noch die 0,25 mit 100 % multiplizieren und natürlich nicht vergessen, das % hinten dran zu schreiben. Das Ergebnis lautet somit:
\text{Prozentsatz}=\text{25} \%
Antwort: 50 (Prozentwert) von 200 (Grundwert) sind also 25 % (Prozentsatz).
Immer noch nicht verstanden? Hier eine noch einfachere Erklärung.
Grundwert: 50 sind 25 % von wie viel?
Wenn wir wissen, dass 50 genau 25 % von „Etwas“ sind, dann bezeichnet man dieses Etwas als Grundwert. Und diesen kann man ausrechnen. Entweder mit unserem Grundwert-ermitteln-Rechner, oder man lernt einfach, wie man den Grundwert selbst berechnet: Mit unseren Formeln und Erklärungen unter dem Rechner. Es ist ganz leicht, wenn man’s einmal verstanden hat!

Öffnen, um die Formel zu verstehen
Der Grundwert sind somit die 100 Prozent.
Man kann das sogar noch komplizierter ausdrücken: Den Grundwert (G) erhält man, indem man den Prozentwert (W) durch den Prozentsatz (P) dividiert und anschließend mit 100 % multipliziert.
Man kann es sich aber auch ganz einfach machen: Bei der Frage „50 sind 25 % von wie viel“ ist der Grundwert (G) der gesuchte Wert. Der Prozentwert (W) ist 50. Der Prozentsatz ist 25 %.
Damit man sich nur eine Formel merken muss, stellen wir die Ausgangsformel um:
\text{100 \%}\times\text{W}=\text{G}\times\text{P}
Da wir nach G suchen, kommt das auf die linke Seite:
\text{G}\times\text{P}=\text{W}\times\text{100 \%}
Anschließend teilen wir durch P, damit G alleine stehen bleibt. Somit erhalten wir:
\text{Grundwert (G)}=\text{Prozentwert (W)}\times\frac{\text{100} \%}{\text{Prozentsatz (P)}}
Dann setzen wir einfach die Werte ein:
\text{Grundwert (G)}=\text{50}\times\frac{\text{100} \%}{\text{25 \%}}
Wir wandeln den Bruch in eine ganze Zahl um, indem wir die 100 % durch die 25 % teilen:
\text{Grundwert (G)}=\text{50}\times\text{4}
Und rechnen einfach 50 mal 4. Das Ergebnis lautet somit:
\text{Grundwert}=\text{200}
Antwort: 50 (Prozentwert) sind also 25 % (Prozentsatz) von 200 (Grundwert)!
Noch nicht verstanden? Hier eine noch einfachere Erklärung.
Berechnung von Prozenten bei Veränderungen und Vergleichen
Bei Prozentrechnungen, wie wir sie oben beschrieben haben (Berechnung von Grundwert, Prozentwert und Prozentsatz), möchten wir wissen, wie viel ein Teil vom Ganzen ist.
Manchmal möchten wir aber berechnen, wie sich Dinge verändert haben – ob sie größer oder kleiner geworden sind. Der folgende Abschnitt behandelt solche Berechnungen.
Preise können steigen oder sinken. Wir verwenden Prozente, um diese Veränderungen zu beschreiben. Wenn etwas teurer wird, sagen wir, es ist um einen bestimmten Prozentsatz gestiegen. Wenn es billiger wird, sagen wir, es ist um einen bestimmten Prozentsatz gesunken.
Preise ändern sich oft im Alltag. Zum Beispiel, wenn eine Pizza früher 10 Euro gekostet hat und jetzt 12 Euro kostet, ist der Preis um 20 % gestiegen.
In der Geschäftswelt schauen sich die Leute auch an, wie gut oder schlecht etwas im Vergleich zu früher ist. Sie vergleichen es mit dem, was im letzten Monat, den letzten drei Monaten oder dem letzten Jahr passiert ist, und berechnen die Veränderung in Prozent.
Beispiele hierfür sind Aussagen wie: „In dieser Firma sind 30 % mehr Männer als Frauen beschäftigt.“ Oder: „Dieses Jahr nahmen 28 % weniger Wähler an der Bundestagswahl teil als im Vorjahr.“ Oder: „Von Schuhgröße 40 zu 41 sind 0,67 cm – Wie vielen Prozent entspricht das?“
Von Wert zu Wert: Wie viel Prozent mehr/weniger sind 200 als 50?
Mit unserem Wert-zu-Wert-Prozentrechner kannst du prozentuale Unterschiede zwischen zwei Zahlen ganz einfach berechnen. Du kannst dir aber auch die Formeln unter dem Rechner anschauen, um zu lernen, wie du das Ganze selbst ausrechnest.
Grundsätzlich kann man auch diese Berechnung mit der Ausgangsformel durchführen. Es gibt aber eine vereinfachte Formel, die man sich besser merken kann. Dabei unterscheidet man die Frage, um wie viel Prozent ein Wert größer ist als ein anderer – und die Frage, um wie viel Prozent ein Wert kleiner ist als ein anderer.
Formel für den Fall: Wie viel Prozent sind 200 mehr als 50?
Formel für den Fall: Wie viel Prozent sind 50 kleiner als 200?
Öffnen, um die Formeln zu verstehen
Es wird also ein prozentualer Anstieg gesucht. Die Formel für den prozentualen Anstieg lautet:
\text{Prozentualer Anstieg}=(\frac{\text{Hoher Wert}}{\text{Kleiner Wert}}-\text{1 })\times\text{100 \% }
Der kleine Wert 50 und der hohe Wert ist 200. Setzen wir diese Werte in die Formel ein, erhalten wir:
\text{Prozentualer Anstieg}=(\frac{\text{200}}{\text{50}}-\text{1 })\times\text{100 \% }
200 geteilt durch 50 sind 4, wir setzen dies ein:
\text{Prozentualer Anstieg}=(\text{4}-\text{1 })\times\text{100 \% }
Und erhalten somit:
\text{Prozentualer Anstieg}=\text{300 \% }
Hä, warum ist der prozentuale Unterschied nicht 400 %? Der Prozentsatz P (also der Anteil von 200 an 50) beträgt zwar 400 %. Aber wir wollen ja die Erhöhung bzw. Reduzierung berechnen. Hierfür müssen wir noch den Grundwert (= 100 %) abziehen. Somit ist das eine Erhöhung um 400 % – 100 % = 300 %.
Für Reduzierungen verhält sich die Formel wie folgt:
Für den Fall „Wie viel Prozent sind 50 kleiner als 200?“ ist der hohe Wert 200 und der kleine Wert 50. Diese Werte muss man einfach wie oben gezeigt in die Formel einsetzen, dann erhält man als Ergebnis -75 %. Das „Minus“ steht hierbei für eine Reduzierung.
In Formeln dargestellt, sähe der Rechenweg so aus:
\text{Prozentuale Reduzierung}=(\frac{\text{50}}{\text{200}}-\text{1 })\times\text{100 \% }
\text{Prozentuale Reduzierung}=(\text{0,25}-\text{1 })\times\text{100 \% }
\text{Prozentuale Reduzierung}=\text{-0,75}\times\text{100 \% }
\text{Prozentuale Reduzierung}=\text{-75 \% }
Prozent abziehen oder aufschlagen: Wie viel sind 50 zuzüglich oder abzüglich 25 %?
Du kannst entweder mit unserem Prozent-Auf-und-Abschlag-Rechner die Abnahme oder Zunahme ausrechnen. Oder du kannst wirklich lernen, wie die Berechnung funktioniert. Schau dir dafür einfach die Formeln und Erklärungen unter dem Rechner an.
Wenn ein Pullover 50 Euro kostet und ich bekomme 25 % Rabatt: Wie viel kostet mich der Pullover dann?
Mit dieser Berechnung beschäftigen wir uns hier. Bei 50 % von oder auf 100 ist es ganz einfach, das bekommt jeder noch hin:
- Prozent aufschlagen: 50 % auf 100 sind 150
- Prozent abziehen: 50 % von 100 sind 50
Auch 100 % von oder auf 100 sind ganz klar:
- Prozent aufschlagen: 100 % auf 100 sind 200
- Prozent abziehen: 100 % von 100 sind 0
Aber bei Werten wie 25 % oder noch schwierigeren Prozentzahlen ist es bei den meisten Menschen mit den Rechenkünsten vorbei. Wenn auch du dazu gehörst, keine Sorge, wir helfen dir bei der Berechnung:
Die Formel für den Fall: Wie viel sind 50 zuzüglich 25 % ?
Die Formel für den Fall: Wie viel sind 50 abzüglich 25 % ?
Öffnen, um die Formeln zu verstehen
Das bedeutet, wir suchen also den Prozentwert! Wieder können wir die Standardformel für die Ermittlung des Prozentwertes verwenden:
\text{Prozentwert (W)}=\text{Grundwert(G)}\times\frac{\text{Prozentsatz(P)}}{\text{100} \%}
Für den Fall „Wie viel sind 50 zuzüglich 25 % ?“ ist der Grundwert 50 und der Prozentsatz ist 125 %. Setzen wir diese Werte in die Formel ein, erhalten wir:
\text{Prozentwert (W)}=\text{50}\times\frac{\text{125} \%}{\text{100} \%}
125 geteilt durch 100 sind 1,25. Wir setzen dies ein:
\text{Prozentwert (W)}=\text{50}\times\text{1,25}
Und erhalten somit:
\text{Prozentwert (W)}=\text{62,5}
Antwort: 50 (Grundwert) zuzüglich 25 % (Prozentsatz) sind also 62,5 (Prozentwert).
Für Reduzierungen verhält sich die Formel genauso:
Für den Fall „Wie viel sind 50 abzüglich 25 %?“ ist der Grundwert 50 und der Prozentsatz ist 75 %. Wieder müssen diese Werte wie oben gezeigt in die Formel eingesetzt werden, das Ergebnis ist entsprechend 37,5.
In Formeln ausgedrückt:
\text{Prozentwert (W)}=\text{50}\times\frac{\text{75} \%}{\text{100} \%}
\text{Prozentwert (W)}=\text{50}\times\text{0,75}
\text{Prozentwert (W)}=\text{37,5}
Um auf unser Beispiel zurückzukommen: Der Pullover, der ursprünglich 50 Euro gekostet hätte, kostet mit 25 % Rabatt nur noch 37,50 Euro. Ein echtes Schnäppchen!
Ausgangswert finden: 200 sind 25 % mehr/weniger als wie viel?
200 sind 100 % mehr als wie viel? 200 sind doppelt so viel wie 100, also 100 % mehr. Die Antwort ist somit 100.
Das bekommt man noch im Kopf ausgerechnet, oder? Für alles andere kannst du einfach unseren Ausgangswert-finden-Prozent-Rechner nutzen. Oder dich packt der Ehrgeiz und du willst lernen, wie du es selbst ausrechnest. Kannst du auch: mit unseren Formeln und Erklärungen direkt unter dem Rechner.
Die Formel für den Fall: 200 sind 25 % mehr als wie viel?
Die Formel für den Fall: 200 sind 25 % weniger als wie viel?
Öffnen, um die Formeln zu verstehen
In kompliziert ausgedrückt, fragt mach sich hier, wenn 100 % + 25 % (Prozentsatz) gleich 200 (Prozentwert) sind, wie groß ist dann der Grundwert.
Die Formel, um den Grundwert auszurechnen, kennen wir bereits von weiter oben:
\text{Grundwert (G)}=\frac{\text{Prozentwert (W)}}{\text{100} \%+\text{Prozentsatz (P)}}
Für den Fall „200 sind 25 % mehr als wie viel?“ ist der Prozentwert 200 und der Prozentsatz ist 25 %. Setzen wir diese Werte in die Formel ein, erhalten wir:
\text{Grundwert (G)}=\frac{\text{200}}{\text{100} \%+\text{25} \%}
Erst rechnen wir
\text{Grundwert (G)}=\frac{\text{200}}{\text{125} \%}
Das entspricht:
\text{Grundwert (G)}=\frac{\text{200}}{\text{1,25 }}
Und erhalten somit:
\text{Grundwert (G)}=\text{160}
Antwort: 200 (Prozentwert) sind also 25 % (Prozentsatz) mehr als 160 (Grundwert).
Für die Frage „200 sind 25 % weniger als wie viel?“ verhält sich die Formel analog:
\text{Grundwert (G)}=\frac{\text{Prozentwert (W)}}{\text{100} \%-\text{Prozentsatz (P)}}
Der Prozentwert ist wieder 200 und es wird diesmal durch 75 % (100% – 25%) geteilt.
\text{Grundwert (G)}=\frac{\text{Prozentwert (W)}}{\text{100} \%-\text{25} \%}
\text{Grundwert (G)}=\frac{\text{200}}{\text{0,75}}
Und erhalten somit:
\text{Grundwert (G)}=\text{266,67}
Antwort: 200 (Prozentwert) sind also 25 % (Prozentsatz) weniger als 266,67 (Grundwert).

Du bist am Ende der Seite angekommen. Was willst du tun?

